RoFormer

RoFormer: Enhanced Transformer with Rotary Position Embeddi

contributions

  • 提出一种相对位置：旋转位置嵌入（RoPE），通过旋转矩阵编码相对位置
  • 研究RoPE的特性，并表明它随相对距离的增加而衰减。之前的相对位置编码方式与线性自注意力不兼容。
  • 在长文本数据集上进行测试

基于的工作

  • 绝对位置编码
    ft(xi,i)=Wt(xi+pi)f_t(x_i, i) = W_t(x_i + p_i)

    {pi,2t=sin⁡(k/100002t/d)pi,2t+1=cos⁡(k/100002t/d)\left\{\begin{matrix} p_{i,2t} & = \sin{(k/10000^{2t/d})} \\ p_{i,2t+1} &= \cos{(k/10000^{2t/d})} \end{matrix}\right.

  • 相对位置编码
    {fq(xm)=Wqxmfk(xn,n)=Wk(xn+p^rk)fv(xnn)=Wv(xn+p^rk)\left\{\begin{matrix} f_q(x_m) = W_qx_m \\ f_k(x_n, n) = W_k(x_n + \hat{p}_r^k) \\ f_v(x_n n) = W_v(x_n + \hat{p}_r^k) \end{matrix}\right.

    • 核心思想是将绝对位置编码的正弦项进行替换。对 k,vk,v 添加可学习的相对位置编码，q不添加偏移量。 rr 表示相对距离.

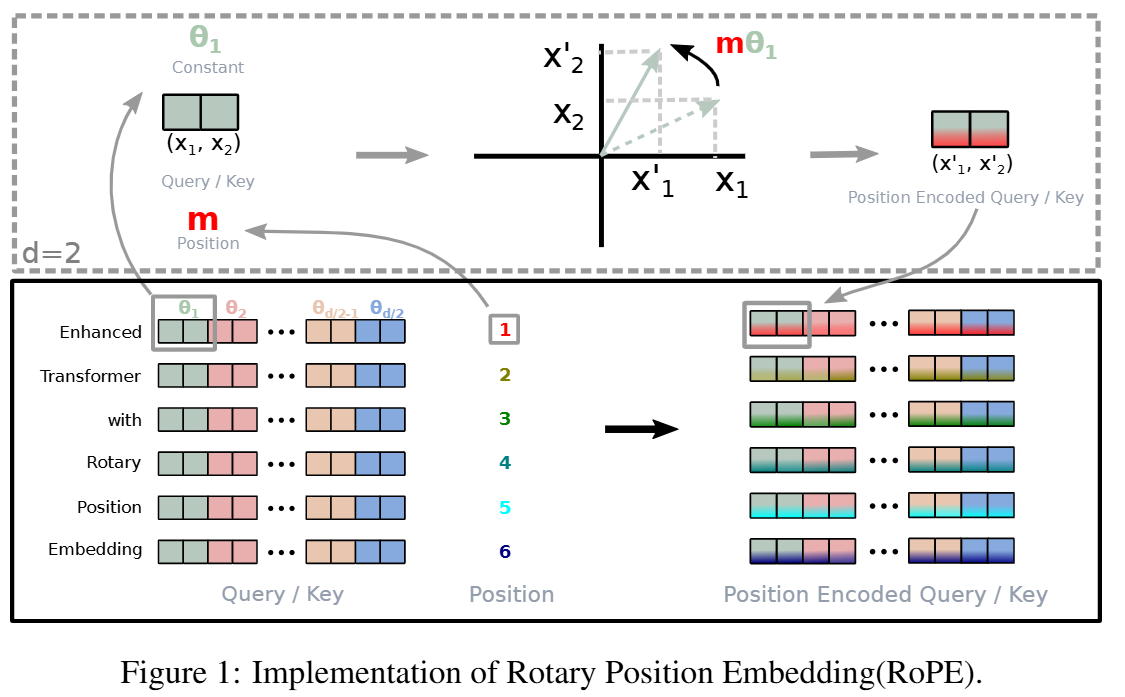
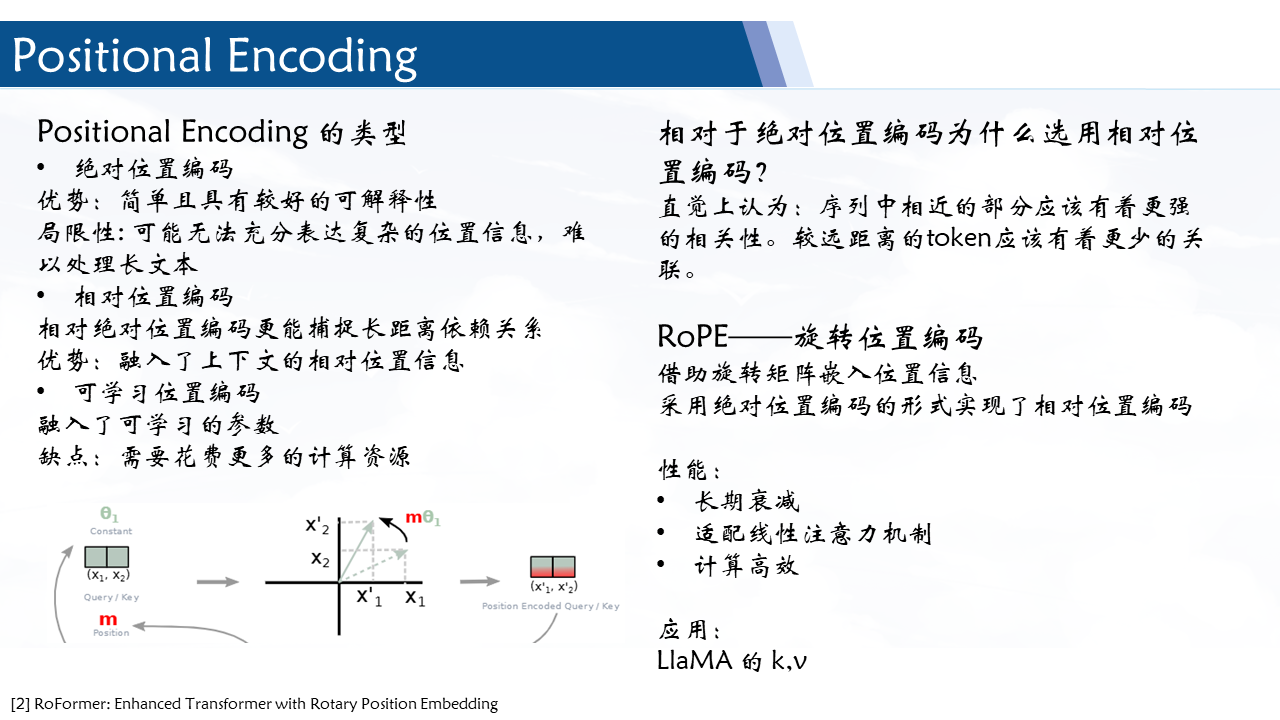
RoPE 旋转位置嵌入

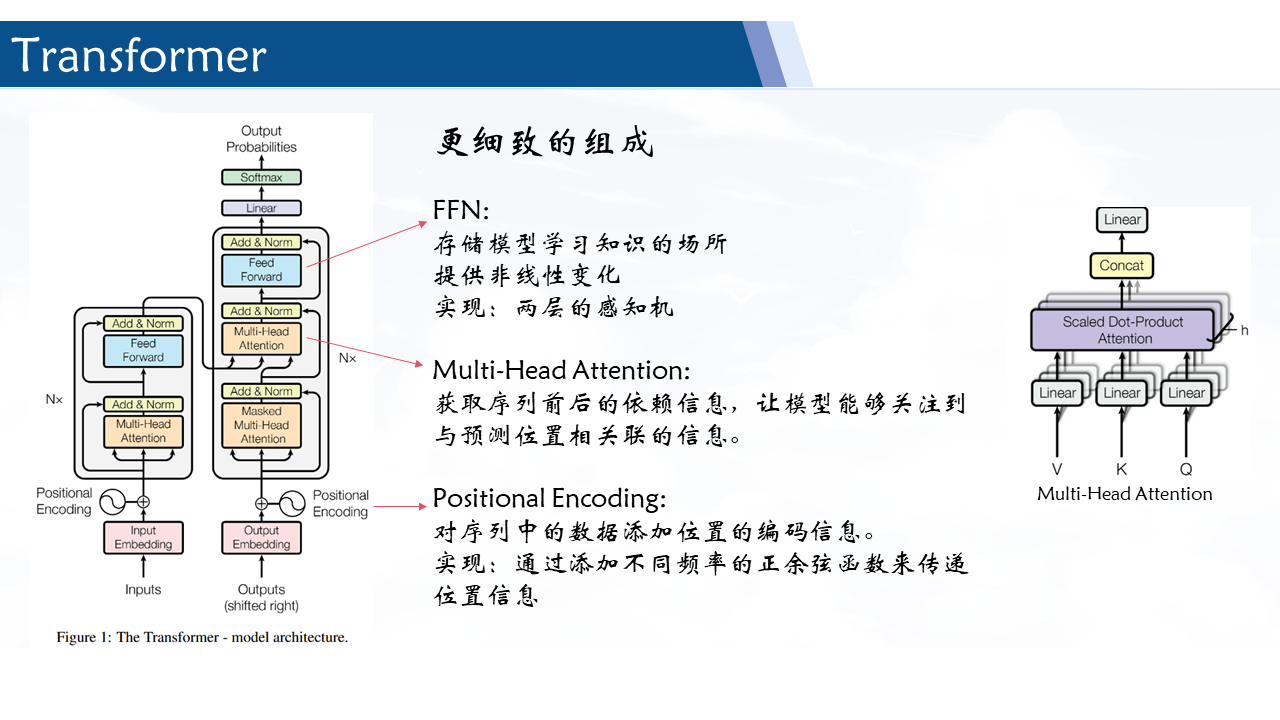
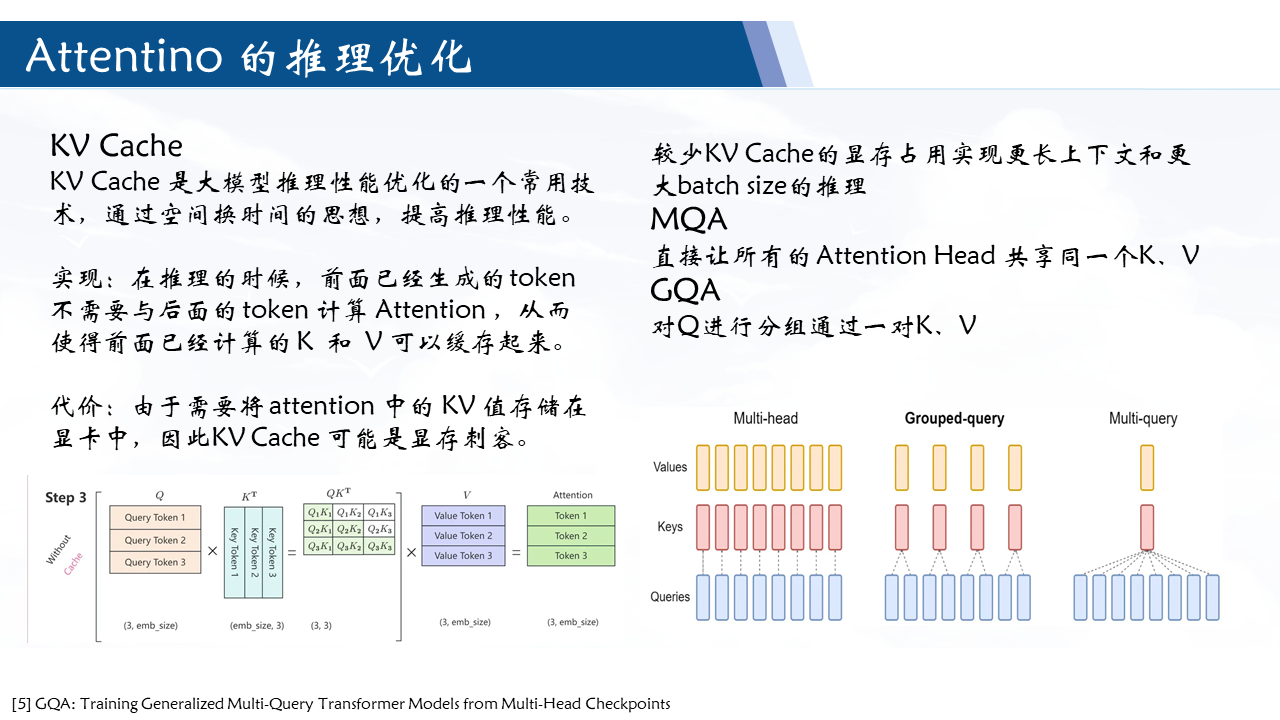
Transformer为基础的模型主要通过attention 来传递位置信息。

Attention(Q,K,V)=Softmax(QKT⊙Mdk)VAttention(Q,K,V) = Softmax(\dfrac{QK^T\odot M}{\sqrt{d_k}})V

由公式不难发现其通过 qmTknq^T_mk_n 来实现不同位置 tokens 之间的信息传递。因此我们希望内积能以融入相对位置的编码信息，即：

<fq(xm,m),fk(xn,n)>=g(xm,xn,m−n)\left<f_q(x_m,m),f_k(x_n,n)\right> = g(x_m, x_n, m-n)

2D实现

借助复数的特性，设计编码函数

fq(xm)=(Wqxm)eimθfk(xn,n)=(Wkxm)einθg(xm,xn,m−n)=Re[(Wqxm)(Wkxm)∗ei(m−n)θ]\begin{array}{c} f_q(x_m) = (W_qx_m)e^{im\theta} \\ f_k(x_n, n) = (W_kx_m)e^{in\theta} \\ g(x_m, x_n, m-n) = \text{Re}\left[(W_qx_m)(W_kx_m)^*e^{i(m-n)\theta}\right] \end{array}

写为旋转矩阵的形式：

f{q,k}(xm,m)=(cos⁡mθ−sin⁡mθsin⁡mθcos⁡mθ)(W{q,k}(11)W{q,k}(12)W{q,k}(21)W{q,k}(22))(xm(1)xm(2))f_{\{q, k\}}\left(\boldsymbol{x}_{m}, m\right)=\left(\begin{array}{cc} \cos m \theta & -\sin m \theta \\ \sin m \theta & \cos m \theta \end{array}\right)\left(\begin{array}{ll} W_{\{q, k\}}^{(11)} & W_{\{q, k\}}^{(12)} \\ W_{\{q, k\}}^{(21)} & W_{\{q, k\}}^{(22)} \end{array}\right)\binom{x_{m}^{(1)}}{x_{m}^{(2)}}

拓展为一般形式

f{q,k}(xm,m)=RΘ,mdW{q,k}xmf_{\{q, k\}}\left(\boldsymbol{x}_{m}, m\right)=\boldsymbol{R}_{\Theta, m}^{d} \boldsymbol{W}_{\{q, k\}} \boldsymbol{x}_{m}

RΘ,md=(cos⁡mθ1−sin⁡mθ100⋯00sin⁡mθ1cos⁡mθ100⋯0000cos⁡mθ2−sin⁡mθ2⋯0000sin⁡mθ2cos⁡mθ2⋯00⋮⋮⋮⋮⋱⋮⋮0000⋯cos⁡mθd/2−sin⁡mθd/20000⋯sin⁡mθd/2cos⁡mθd/2)\scriptsize \begin{array}{c} \boldsymbol{R}_{\Theta, m}^{d}=\left(\begin{array}{ccccccc} \cos m \theta_{1} & -\sin m \theta_{1} & 0 & 0 & \cdots & 0 & 0 \\ \sin m \theta_{1} & \cos m \theta_{1} & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & \cos m \theta_{2} & -\sin m \theta_{2} & \cdots & 0 & 0 \\ 0 & 0 & \sin m \theta_{2} & \cos m \theta_{2} & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & \cos m \theta_{d / 2} & -\sin m \theta_{d / 2} \\ 0 & 0 & 0 & 0 & \cdots & \sin m \theta_{d / 2} & \cos m \theta_{d / 2} \end{array}\right) \end{array}

其中 dd 为而偶数, Θ={θi=10000−2(i−1)/d,i∈[1,2,…,d/2]}\Theta=\left\{\theta_{i}=10000^{-2(i-1) / d}, i \in[1,2, \ldots, d / 2]\right\} , 应用于self-attention 可以得到：

qm⊤kn=(RΘ,mdWqxm)⊤(RΘ,ndWkxn)=x⊤WqRΘ,n−mdWkxn\boldsymbol{q}_{m}^{\top} \boldsymbol{k}_{n}=\left(\boldsymbol{R}_{\Theta, m}^{d} \boldsymbol{W}_{q} \boldsymbol{x}_{m}\right)^{\top}\left(\boldsymbol{R}_{\Theta, n}^{d} \boldsymbol{W}_{k} \boldsymbol{x}_{n}\right)=\boldsymbol{x}^{\top} \boldsymbol{W}_{q} R_{\Theta, n-m}^{d} \boldsymbol{W}_{k} \boldsymbol{x}_{n}

使用乘法，通过旋转矩阵乘积合并相对位置信息。

特性

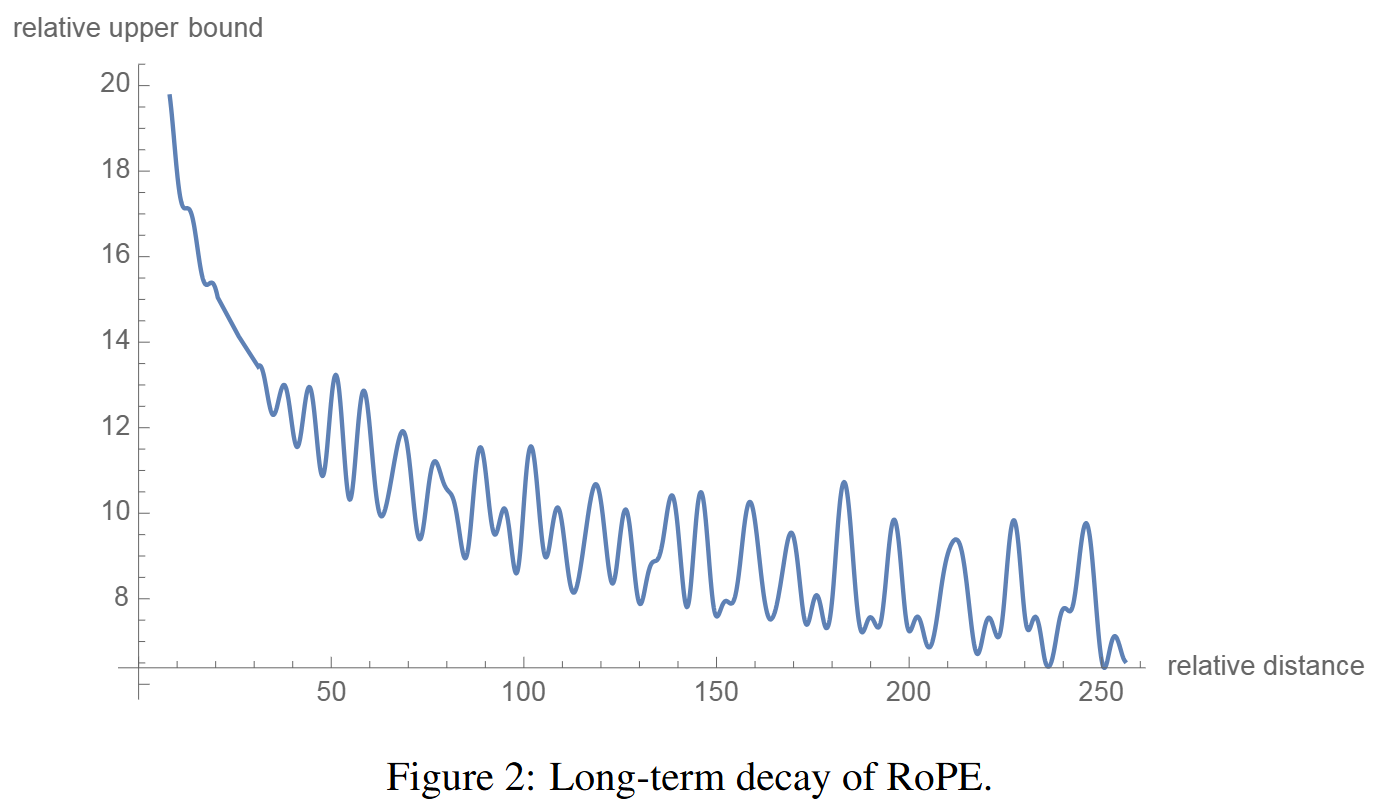
  • 长期衰减：设置 θi=10000−2i/d\theta_i = 10000^{-2i/d} 其提供了长期衰减的特性。随着相对距离的增加，内积会不断衰减。（更远的距离提供更少的关联）
  • 具备线性注意力机制：能够将线性注意力写为更通用的形式

Attention⁡(Q,K,V)m=∑n−1Nϕ(qm)⊤φ(kn)vn∑n−1Nϕ(qm)⊤φ(kn)⇓Attention⁡(Q,K,V)m=∑n−1N(RΘ,mdϕ(qm))⊤(RΘ,ndφ(kn))vn∑n−1Nϕ(qm)⊤φ(kn)\small \begin{array}{c} \operatorname{Attention}(\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V})_{m}=\dfrac{\sum_{n-1}^{N} \phi\left(\boldsymbol{q}_{m}\right)^{\top} \varphi\left(\boldsymbol{k}_{n}\right) \boldsymbol{v}_{n}}{\sum_{n-1}^{N} \phi\left(\boldsymbol{q}_{m}\right)^{\top} \varphi\left(\boldsymbol{k}_{n}\right)} \\ \Downarrow \\ \operatorname{Attention}(\mathbf{Q}, \mathbf{K}, \mathbf{V})_{m}=\dfrac{\sum_{n-1}^{N}\left(\boldsymbol{R}_{\Theta, m}^{d} \phi\left(\boldsymbol{q}_{m}\right)\right)^{\top}\left(\boldsymbol{R}_{\Theta, n}^{d} \varphi\left(\boldsymbol{k}_{n}\right)\right) \boldsymbol{v}_{n}}{\sum_{n-1}^{N} \phi\left(\boldsymbol{q}_{m}\right)^{\top} \varphi\left(\boldsymbol{k}_{n}\right)} \end{array}

ϕ(x)=φ(x)=elu(x)+1\phi(x)=\varphi(x) = \text{elu}(x) + 1

实现更高效的计算

RΘ,mdx=(x1x2x3x4⋮xd−1xd)⊕(cos⁡mθ1cos⁡mθ1cos⁡mθ2cos⁡mθ2⋮cos⁡mθd/2cos⁡mθd/2)+(−x2x1−x4x3⋮−xdxd−1)⊕(sin⁡mθ1sin⁡mθ1sin⁡mθ2sin⁡mθ2⋮sin⁡mθd/2sin⁡mθd/2)\small \boldsymbol{R}_{\Theta, m}^{d}\boldsymbol{x} = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ \vdots\\ x_{d-1} \\ x_d \\ \end{pmatrix} \oplus \begin{pmatrix} \cos m\theta_1 \\ \cos m\theta_1 \\ \cos m\theta_2 \\ \cos m\theta_2 \\ \vdots \\ \cos m\theta_{d/2} \\ \cos m\theta_{d/2} \\ \end{pmatrix} + \begin{pmatrix} -x_2 \\ x_1 \\ -x_4 \\ x_3 \\ \vdots\\ -x_d \\ x_{d-1 }\\ \end{pmatrix} \oplus \begin{pmatrix} \sin m\theta_1 \\ \sin m\theta_1 \\ \sin m\theta_2 \\ \sin m\theta_2 \\ \vdots \\ \sin m\theta_{d/2} \\ \sin m\theta_{d/2} \\ \end{pmatrix}

性能测试

  • 机器翻译-blue
  • 预训练-损失下降更快
  • GLUE 任务
  • 中文数据集——更强的长文本能力

代码实现

RoPE
1
def

Scaling Laws for Neural Language Models

L(D,N,P)≈A∗N−α+B∗D−β+C−γL(D, N, P) \approx A*N^{-\alpha} + B*D^{-\beta} + C^{-\gamma}

符号 含义 单位/类型
LL 损失函数值 无单位（标量）
DD 训练数据量 Token 数
CC 计算资源 FLOPs（浮点运算次数）
NN 模型参数规模 参数量（如亿、万亿）
α,β,γ\alpha, \beta, \gamma 原始公式的经验系数

Switch Transformers

Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity

contributions

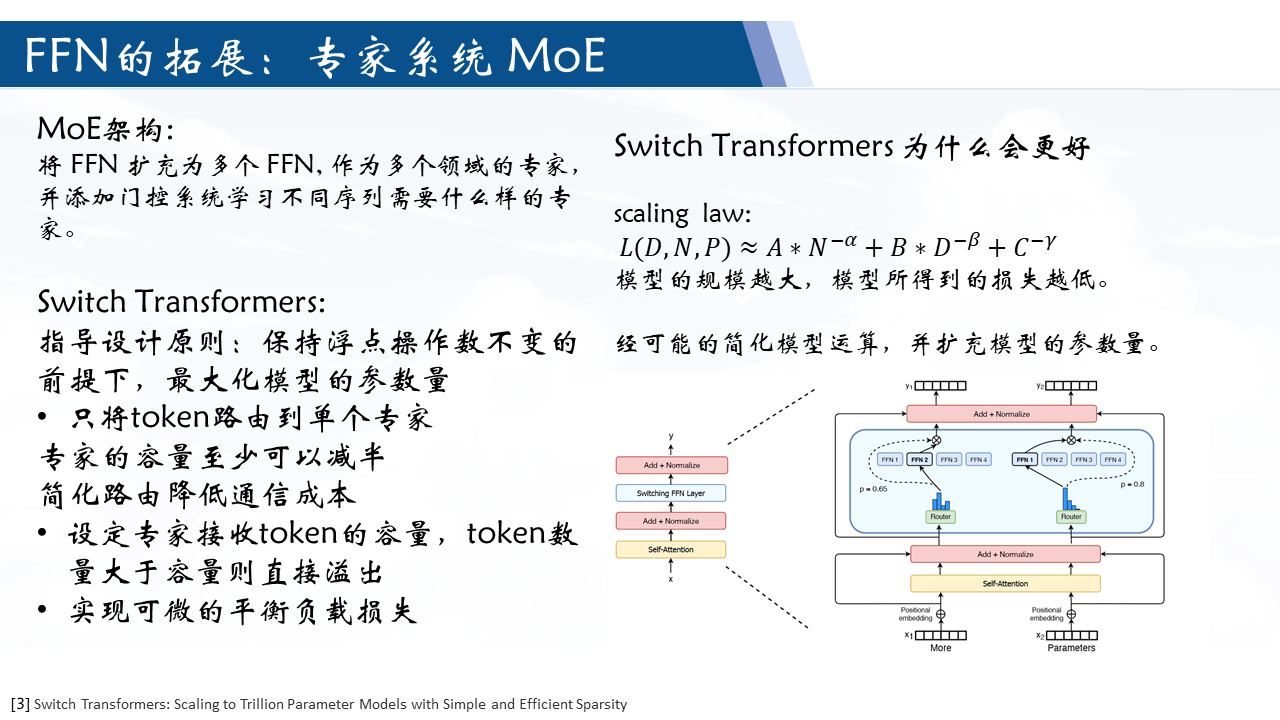
  • 提出 Switch Transformer 结构——对 MoE 的简化和改进
  • Switch Transformer 有效性证明
  • 预训练和微调技术的改进
    • 选取 float16
    • 运行扩展到更多专家的方案
    • 增加专家正则化来改善稀疏模型的微调和多任务训练
  • 多语言数据的预训练收益
  • 扩大了模型的大小且提高模型的预训练速度

Switch Transformer

指导设计原则：最大化模型的参数量

在保持浮点操作 FLOP（运算次数）不变的前提下，增加参数的数量

在 MoE 框架下的改变：

  • 只将token路由到单个专家
  • 专家的容量至少可以减半
  • 简化路由降低通信成本

高效稀疏路由：

专家容量=(批量大小专家数量)×容量系数专家容量 =\left(\dfrac{批量大小}{专家数量}\right) \times 容量系数

其为每个batch的tokens分配一个专家，若一个专家接收的token大于专家容量，则直接跳过计算（不通过该专家）通过残差连接进入下一层。

可微的平衡负载损失：

loss=α⋅N⋅∑i=1Nfi⋅Pi\text{loss} = \alpha \cdot N\cdot\sum\limits_{i=1}^N f_i\cdot P_i

其中 α\alpha 为超参数， NN 为专家数量,

fif_i 为分配给专家 ii 的 token 比例： fi=1T∑x∈B[arg max⁡p(x)=i]f_i = \dfrac{1}{T}\sum\limits_{x\in B}[\argmax p(x) = i]

PiP_i 为分配给专家 ii 的路由的概率： Pi=1T∑x∈Bpi(x)P_i = \dfrac{1}{T}\sum\limits_{x\in B}p_i(x)

Training and Fine-Tuning

  • 在路由器输入时转化为 float32 进行计算
  • 实现蒸馏

DEEPSEEKMOE

DEEPSEEKMOE: TOWARDS ULTIMATE EXPERT SPECIAL-IZATION IN MIXTURE-OF-EXPERTS LANGUAGE MODELS

MoE 架构可能遇到的问题：知识混合和知识冗余

contributions

  • 架构创新：提供一种新的 MoE 架构，采用细粒度专家分割和共享专家隔离两种主要策略
  • 实验验证其有效性
  • 稳定性
  • 与 MoE 对齐

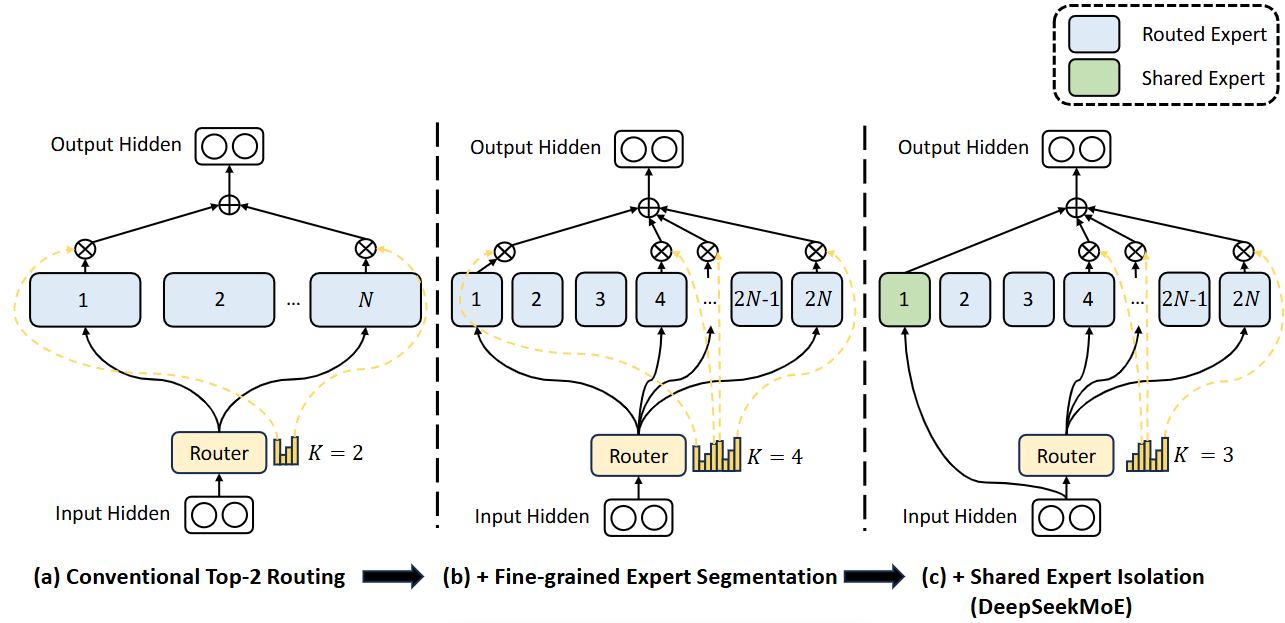
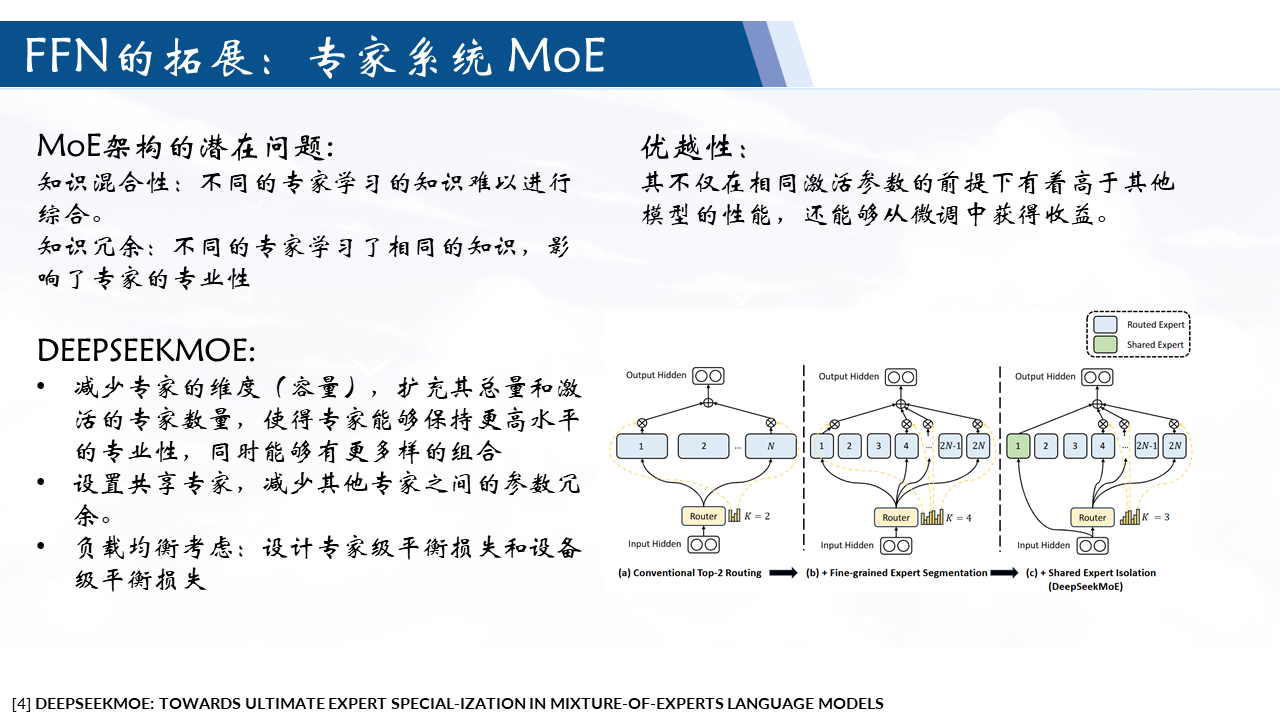
DeepSeekMoE 结构

细粒度专家细分

让不同的知识分布在不同的专家，每位专家可以保持高水平的专家专业化

做法：将专家的参数量减少，增加专家的数量和激活专家的数量。

共享专家隔离

多个专家可能会集中获取各自参数的共享知识，从而导致专家参数的冗余。

共享专家致力于捕获和巩固不同上下文中的共同知识，那么其他路由专家之间的参数冗余将会得到缓解。

做法：设定部分专家为固定的激活的专家

htl=∑i=1KsFFN⁡i(utl)+∑i=Ks+1mN(gi,tFFN⁡i(utl))+utl,gi,t={si,t,si,t∈Topk⁡({sj,t∣Ks+1⩽j⩽mN},mK−Ks),0, otherwise, si,t=Softmax⁡i(utlTeil).\begin{array}{l} \mathbf{h}_{t}^{l}=\sum_{i=1}^{K_{s}} \operatorname{FFN}_{i}\left(\mathbf{u}_{t}^{l}\right)+\sum_{i=K_{s}+1}^{m N}\left(g_{i, t} \operatorname{FFN}_{i}\left(\mathbf{u}_{t}^{l}\right)\right)+\mathbf{u}_{t}^{l}, \\ g_{i, t}=\left\{\begin{array}{ll} s_{i, t}, & s_{i, t} \in \operatorname{Topk}\left(\left\{s_{j, t} \mid K_{s}+1 \leqslant j \leqslant m N\right\}, m K-K_{s}\right), \\ 0, & \text { otherwise, } \end{array}\right. \\ s_{i, t}=\operatorname{Softmax}_{i}\left(\mathbf{u}_{t}^{l^{T}} \mathbf{e}_{i}^{l}\right) . \end{array}

均衡负载

模型总是只选择少数专家，导致其他专家无法得到充分的训练。其次，如果专家分布在多个设备上，负载不平衡会加剧计算瓶颈。

专家级均衡损失

LExpBal =α1∑i=1N′fiPi,fi=N′K′T∑t=1T1( Token t selects Expert i),Pi=1T∑t=1Tsi,t,\begin{aligned} \mathcal{L}_{\text {ExpBal }} & =\alpha_{1} \sum_{i=1}^{N^{\prime}} f_{i} P_{i}, \\ f_{i} & =\frac{N^{\prime}}{K^{\prime} T} \sum_{t=1}^{T} \mathbb{1}(\text { Token } t \text { selects Expert } i), \\ P_{i} & =\frac{1}{T} \sum_{t=1}^{T} s_{i, t}, \end{aligned}

N′=mN−KsN' = mN - K_s, K′=mK−KsK' = mK - K_s

设备级均衡损失

LDevBal =α2∑i=1Dfi′Pi′,fi′=1εi∣∑j∈εifi,Pi′=∑j∈εiPj,\begin{aligned} \mathcal{L}_{\text {DevBal }} & =\alpha_{2} \sum_{i=1}^{D} f'_{i} P'_{i}, \\ f'_{i} & =\frac{1}{\varepsilon_i|} \sum_{j \in \varepsilon_i}f_i, \\ P'_{i} & = \sum_{j \in \varepsilon_i} P_j, \end{aligned}

PPT知识汇总

pdf-linkhttps://www.pan.hekaiyu.com.cn/d/file/%E7%A7%91%E7%A0%94/%E5%A4%A7%E8%AF%AD%E8%A8%80%E6%A8%A1%E5%9E%8B%E7%BB%93%E6%9E%84/%E8%AE%BA%E6%96%87%E9%98%85%E8%AF%BB.pdf?sign=s6iqm2Oz-abFSgnRM4BP-FyQqIn22XabLQK2MANxa5g=:0
许可协议

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。

分享文章

快来参与讨论吧~