绪论

机器学习三要素：模型、学习准则、优化算法

评估方法

• 留出法：直接将数据集划分为两个互斥的集合，其中一个为训练集，另一个为测试集。
• 交叉验证：
• 自助法：随机抽取m个样本进行进行训练，其余的用于模型评估（测试集）

训练集：用于模型学习
验证集：用于调参和模型评估
测试集：用于测试模型性能

贝叶斯公式

最小错误率贝叶斯决策

后验概率 $P(\omega_1 | x) = \dfrac{P(x|\omega_1)P(\omega_1)}{\sum P(x|\omega_j)P(\omega_j)}$
$P(\omega_1)$——先验概率，$P(x|\omega_1)$——似然概率

最小风险贝叶斯决策

考虑不同决策带来的损失 $R(\alpha_i|x) = \sum \lambda_{ij}P(\omega_j|x)$

半朴素贝叶斯分类器

独依赖估计： 每个属性在类别之外仅依赖一个其他属性

父属性的确认方法：

• SPODE方法：所有属性都依赖于同一个属性
• AODE方法：将每个属性都作为超父属性来构建SPODE

贝叶斯网络

所有属性之间均可存在依赖关系，使用有向无环图表示

ROC曲线

真阳性率TPR~假阳性率FPR

$TPR = \dfrac{TP}{TP+ FN}$

$FPR = \dfrac{FP}{FP+ FN}$

作用：

• 确定似然比
• 比较两种分类判别方法的性能
• 作为特征与类别相关性的度量
• 越靠近左上角越好（计算面积——AUC分数）

概率密度函数估计（求解先验概率）

极大似然估计$\theta$是确定的、未知的

原理：使样本集出现的概率最大

步骤：

• 构造似然函数 $l( \theta ) = \Pi P(x_i|\theta)$
• 取对数 $\ln l(\theta)$
• 求偏导，求最大值

非参数估计 $P(x) = \frac{K_N}{NV_N}$

$K_N$ 是 $N$ 个样本落 $V_N$ 的样本数

收敛条件：

• $\lim\limits_{N\to\infty}V_N = 0$
• $\lim\limits_{N\to\infty}K_N = \infty$
• $\lim\limits_{N\to\infty}\dfrac{K_N}{N} = 0$

Parzen 窗口估计法

样本足够多才能有较好估计

对 $V_N$ 作限制，如 $V_N = \dfrac{h}{\sqrt{n}}$
$P_N = \dfrac{1}{N} \sum\limits_{i=1}^N\dfrac{1}{V_N}\varphi (\frac{x-x_i}{h_N})$

$K_N$ 近邻法

$K_N$ 作限制，如 $K_N = \sqrt{N}$, $V_N = \frac{V_1}{\sqrt{N}}$

线性模型

线性判别函数： $g(x) = w^Tx+ w_0$

将 $x$ 替换为 $\varphi(x)$

Fisher 线性判别分析

思路：类内离散度尽可能小，类间离散度尽可能大

方法：拉格朗日乘数法

准则函数 $J(w) = \dfrac{w^TS_bw}{w^TS_ww}$

步骤：

• 求均值 $m_i = \dfrac{1}{N}\sum x$

• 求类内离散度矩阵 $S_i = \sum (x -m_i)(x - m_i)^T$

• 总类内离散度矩阵 $S_w = S_1+ S_2$

  类间离散度矩阵 $S_b = (m_1 -m_2)(m_1 - m_2)^T$

• 求 $w^* = S^{-1}_w(m_1-m_2)$

• 求 $w_0 = -\frac{1}{2}w^{*T}(m_1+ m_2)$

• 判别函数 $g(x) = w^{*T}x + w_0$

感知器

样本线性可分

• $y\in w_1$ 时, $g(x)>0$
• $y\in w_2$ 时, $g(x)<0$

步骤：

• 增广化——添加一维并设置为1— $(1,0,1) \to (1,0,1,1)$
• 规范化 $y' = \left\{\begin{matrix} y &\text{if} ~~~~ y\in w_1 \\ -y &\text{if} ~~~~ y\in w_2 \\ \end{matrix}\right.$
• 将样本带入 $g(x) = \alpha^T y$, 若 $g(x) > 0$则不变， 若 $g(x)<0$ 则修正 $\alpha_{i+ 1} = \alpha_i + \rho y_k$

线性回归

• 单变量线性回归
  • 方法：最小二乘法
  • 性能评价：均方误差
• 多元线性回归
  • $E(\hat{w})=(Y-X\hat{w})^T(Y-X\hat{w})$
  • $\hat{w} = (X^TX)^{-1}X^TY$

• $E(\hat{w})=(Y-X\hat{w})^T(Y-X\hat{w})+\frac{1}{2}\lambda\hat{w}^T\hat{w}$
• $\hat{w} = (\lambda I+X^TX)^{-1}X^TY$

对数几率回归 （logitstic 回归）

概率模型 $\begin{cases} P(y=1|x;w,b) = \dfrac{e^{w^Tx+b}}{1+e^{w^Tx+b}} \\ P(y=0|x;w,b) = \dfrac{1}{1+e^{w^Tx+b}} \end{cases}$ 取 $p=P(y=1|x;w,b)$

支持向量机

• 最优分类超平面

能够将训练样本没有错误地分开且两类训练 样本中离平面最近的超平面之间的距离最大（分类间隔）

线性可分支持向量机

对于线性可分数据集，最大间隔分类面存在且唯一

原问题

$$\min\limits_{w,b} \frac{1}{2} \left \| w \right \| ^2\quad s.t.\ \ y_i(w^Tx_i + b) \ge1, \ i=1,2,\cdots, N$$

原问题的对偶问题: 拉格朗日函数的极大极小问题

$$L(w, b, \alpha) =\frac{1}{2} \left \| w \right \| ^2 + \sum\limits_{i=1}^N\alpha _i(1-y_i(w^Tx_i+b)) \\ \max\limits_{\alpha}\min\limits_{w, b} L(w, b, \alpha)\qquad s.t. \ \ \alpha_i \ge 0$$

$$\min\limits_\alpha \frac{1}{2} \sum\limits_{i=1}^n\sum\limits_{j=1}^n \alpha_i \alpha_j y_iy_j(x_i\cdot x_j)- \sum\limits_{i=1}^n \alpha_i \\ s.t. \qquad \alpha_iy_i = 0 \text{且} \alpha_i\ge 0,\ \ i=1,2,\cdots,n$$

线性支持向量机

$$\min\limits_{w,b,\xi} \frac{1}{2} \left \| w \right \| ^2 + C\sum\limits_{i=1}^n \xi_i \\ s.t. y_i(w^Tx_i + b) \ge 1 - \xi_i \ \ (\xi \ge 0), \ i=1,2,\cdots, N$$

$C$ 较大，更关系错分样本；$C$ 较小，更关心分类间隔；选取合适的 C 适当的关注分类间隔能减小过拟合

• 支持向量
  • 决定最优分类超平面的样本
  • 如何寻找
    • 间隔边界上
    • 间隔边界与超平面之间
    • 分类超平面误分类一侧
    • 分类超平面上

非线性支持向量机

引入映射函数，将样本值替换为映射函数 $\varphi(x_i)$

设计核函数—— 定义特征空间中的样本内积

$\kappa (x_i,x_j) = (\phi(x_i)\cdot\phi(x_j))$

如何不用构造映射 $\phi(x)$, 之间判断给定的 $\kappa(x, y )$ 是不是核函数

常用核函数

• 线性核 $x^Ty$
• 多项式 $(x^Ty+r)^p$
• 高斯核 $\exp\left(-\dfrac{\left \| x-y \right \|^2}{2\sigma^2}\right)$
• sigmoid 核 $\tanh (\beta x^Ty+\theta)$

组合已知的核函数，得到新的核函数

• 线性组合
• 函数乘积
• 函数连乘：$g(x)K(x,y)g(y)$

其他分类方法

最近邻法

• 计算训练样本与测试样本的距离
• 选取最近邻者的类别作为决策结果

K-近邻法(KNN)

• 在所 $N$ 个样本中找到与测试样 $k$ 个最近邻的样本
• 选取类别频率最高者作为决策

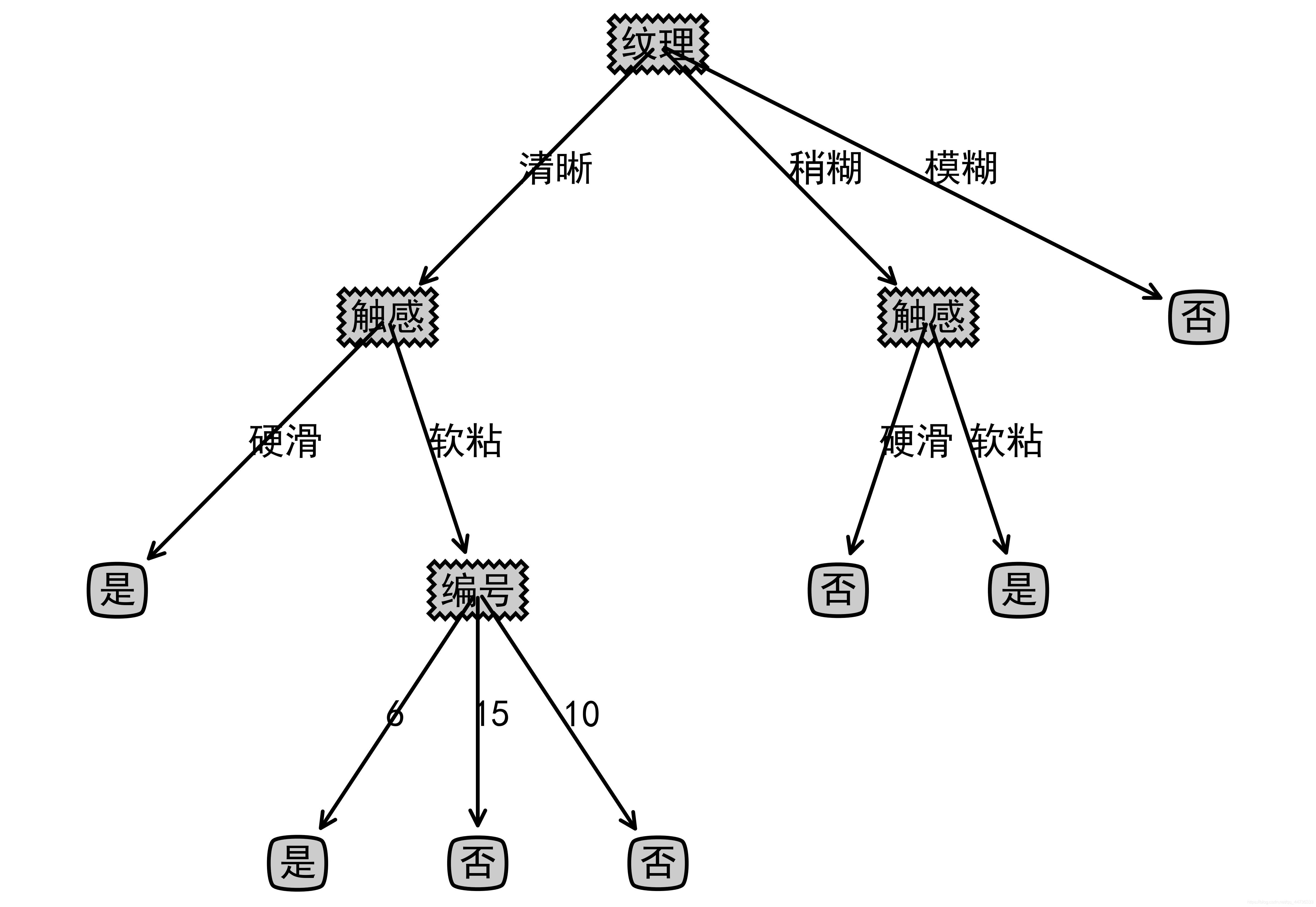
决策树

内部结点——一个特征

叶子结点——分类

特征值选取

选信息增益最大的属性 $g(D,A) = H(D) - H(D|A)$

决策树生成——使用训练样本

• ID3算法 对取值较多的属性有偏好
  • 计算数据集分类前的熵 $H(D) = -\sum\limits_{k=1}^K\dfrac{|C_k|}{|D|}\log_2{\dfrac{|C_k|}{|D|}}$
  • 计算特征A对数据集D的条件熵（子类熵的加权和 $H(D|A)=\sum\limits_{i=1}^n\dfrac{|D_i|}{|D|}H(D_i)$
  • 计算信息增益 $g(D,A) = H(D) - H(D|A)$
  • 选信息增益最大的属性作为结点
• C4.5算法
  • 求特征A的熵 $H_A(D) = -\sum\limits_{i=1}^n\dfrac{|D_i|}{|D|}\log_2{\dfrac{|D_i|}{|D|}}$
  • 求信息增益率 $g_R(D,A) = \dfrac{g(D,A)}{H_A(D)}$
• CART算法
  • 尼基系数 $Gini(D) = 1 - \sum(\dfrac{|C_k|}{|D|})^2$
  • 选基尼指数最小的特征 $Gini(D,A) = \sum\dfrac{|D_i|}{|D|} Gini(D_i)$

决策树剪枝 ——使用测试样本

• 预剪枝
  • 容易欠拟合
  • 从根节点开始
• 后剪枝
  • 从叶子节点开始
• 判断剪枝后是否正确率是否提升，来决定是否删除该节点

连续值处理

二分法：选取最优的分界值对其进行划分

随机森林——构建多个决策树

原理：将样本输入到每个决策树中进行分类，选所有决策中较多决策的结果。

每棵决策树随机选择一个子集进行训练。

特征选择

判据：

• 基于类内类间距离的可分性判据
• 基于概率可分的可分性判据
• 基于熵的可分性判据

分支定界法

• 从包含所有候选特征开始，自顶向上，逐步去掉不被选中的特征。
• 要求：判据对特征具有单调性，某节点函数值小于B直接回溯

特征提取

基于类别可分性判据的特征提取

• 求最优的变换矩阵 $w^*$ ,使可分性判据 $J(x)$ 最大
  • 求均值 $m_i = \dfrac{1}{N}\sum x$
  • 类内离散度矩阵 $S_i = \sum\limits_{i-1}^C P_i\sum\limits_{k=1}^{n_i} (x^i -m_i)(x^i - m_i)^T$
    类间离散度矩阵 $S_b = \sum\limits_{i-1}^C(m_1 -m)(m_1 - m)^T$
  • 求 $A = S_w^{-1}S_b$
  • 求特征值并按从大到小排序
  • 求 $A$ 的特征向量
  • 选取 $d$ 个作为新的特征 $W=[x_1,x_2,\cdots,x_d]$
• 主成分分析法——非监督
• K-L变换（主成分分析的监督实现）
  • 求产生矩阵

    • 类别未知

      $\varphi=E\left[x x^T\right]$

      $\varphi=E\left[(x-\mu)(x-\mu)^T\right]$ ——PCA方法

    • 类别已知

      $\varphi =S_w = \sum\limits_{i=1}^CP_iE\left[(x^i-\mu_i)(x^i-\mu_i)^T\right]$

    • 后续同第一点

非监督——无标签样本分类

• 动态聚类算法——c均值算法
• 分级聚类
  • 初始化每个样本形成一个类
  • 计算两类之间的距离——定义类间距离（最近、最远、均值）
  • 选择最小距离的两类进行合并

多分类问题

• 多对多
  • 对每类样本编码，并比较测试样本与其的距离，选取距离最小者的类别为分类结果
  • 衡量距离的类型：汉明距离、欧氏距离
• 一对一
  • 训练多个二分类器投票决定
• 一对多
  • 预测是否为 $C_i$

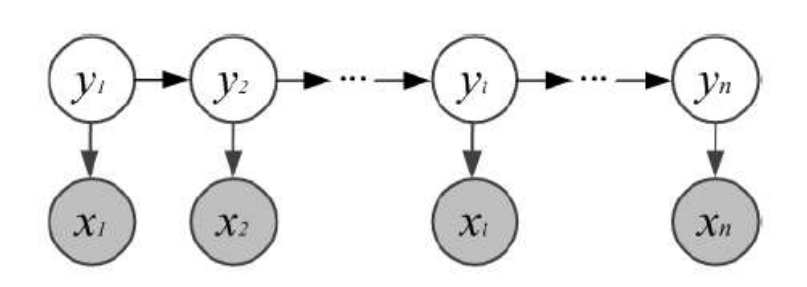
HMM（隐马尔可夫）模型

三要素：

• 初始状态分布 $\pi$
• 状态转移矩阵 $A$
• 观测概率矩阵 $B$

两个基本假设

• 齐次马尔可夫性假设
  系统在任意时刻 $t$的 隐藏状态 $q_t$ 只依赖于其前一时刻的隐藏状态$q_{t−1}$，与更早的状态及观测值无关。
• 观测独立性假设
  任意时刻t的观测值$O_t$仅依赖于该时刻的隐藏状态$q_t$，与其他时刻的隐藏状态或观测值无关。

三个基本问题

• 计算问题：求观测 $P(O|\lambda)$
• 学习问题：只有观察数据求模型
• 解码问题：求状态 $P(I|O,\lambda)$

许可协议

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。

分享文章